As estações do ano em nosso planeta
As estações do ano resultam do fato de que o eixo de rotação da Terra está inclinado por uns 23.5° com relação à normal ao seu plano orbital (plano da eclítica). O eixo aponta sempre na mesma direção no espaço (exceto pelos efeitos secundários de precessão e nutação, que discutiremos mais adiante), de forma que o pólo norte está por vezes inclinado na direção do Sol (de junho a agosto) e por vezes na direção oposta (de dezembro a março). Estas duas situações, obviamente, caracterizam o inverno e verão no Hemisfério Sul da Terra, sendo a situação inversa no Hemisfério Norte.
A figura abaixo procura ilustrar a situação: o Sol é representado pela esfera no centro da figura. A linha horizontal pertence ao plano da órbita da Terra em torno do Sol (este plano é perpendicular à figura). A Terra (esfera menor) é mostrada em duas situações distintas: à esquerda, vemos a Terra no dia do solstício de dezembro. Nesta situação, os raios solares incidem perpendicularmente sobre o Trópico de Capricórnio (= paralelo de latitude φ = -23.5°). Outra maneira de dizer a mesma coisa é que a declinação do Sol é δ = -23.5°. Pelo fato do Sol iluminar mais o Hemisfério Sul, as noites são mais curtas e os dias mais longos neste hemisfério do que no Norte. A incidência mais perpendicular dos raios solares sobre o Hemisfério Sul também ajuda a aquecer as regiões a sul do Equador; inicia-se, portanto, o verão (inverno) no Hemisfério Sul (Norte) geográfico. Já na posição à direita, a Terra está no extremo oposto de sua órbita anual, sendo este então o solstício de junho. A declinação do Sol é agora δ = +23.5° e os raios solares incidem perpendicularmente sobre o Trópico de Câncer (φ = +23.5°) neste dia. Trata-se do início do inverno (verão) no Hemisfério Sul (Norte).
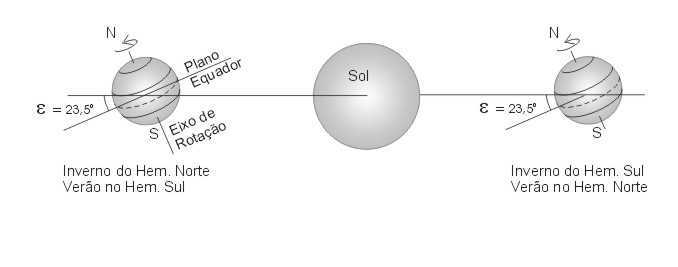
O ângulo de 23.5° entre os plano equatorial e o plano orbital da Terra é chamado de obliqüidade da eclítica, sendo comumente representado pela letra grega epsilon (ε).
Sabemos que o céu muda sazonalmente, havendo constelações visíveis somente no verão ou no inverno em cada hemisfério. Isso ocorre porque, à medida em que o Sol se move pela eclítica (como reflexo do movimento orbital da Terra em seu torno), as estrelas que aparecem no céu noturno (ou seja, que se situam longe do Sol) variam.

Eclipses
Eclipses ocorrem quando a Terra, Sol e Lua se encontram sobre uma linha reta. Podemos então ter duas situações distintas: 1) a Lua se situa entre o Sol e a Terra, projetando sua sombra sobre esta última. 2) a Terra se situa entre o Sol e a Lua, projetando sua sombra sobre esta última. No primeiro caso temos um eclipse solar, no segundo um eclipse lunar. Note que eclipses lunares só ocorrem quando a Lua está na fase cheia, enquanto que os eclipses solares só ocorrem quando a Lua está na fase nova.
Outra diferença é que a sombra da Lua projetada sobre a Terra não cobre toda a superfície desta última. Já a sombra da Terra é suficientemente grande (e a Lua suficientemente pequena) para cobrir toda a Lua. Assim, eclipses solares só são visíveis de alguns pontos da Terra, mas eclipses lunares são visíveis por qualquer observador que tenha a Lua acima do seu horizonte quando ocorrem.
Por que não ocorrem eclipses todo mês?
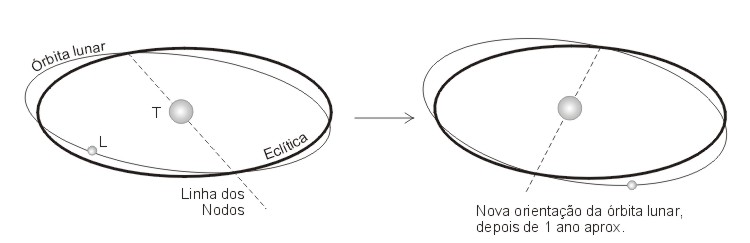
- Por que o plano da órbita da Lua em torno da Terra não coincide com o plano da órbita da Terra em torno do Sol. Uma outra maneira de dizer isso é que a Lua não se move sobre a eclítica, mas sobre um outro grande círculo no céu, que faz um ângulo de 5° com a eclítica.
A linha que conecta os dois pontos de intersecção entre o plano da eclítica e a órbita da Lua é chamada de linha dos nodos. Somente quando a linha dos nodos aponta na direção do Sol podem ocorrer eclipses. Há, portanto, duas época ao longo do ano em que podem ocorrer eclipses. Estas épocas mudam com o tempo devido às perturbações gravitacionais sofridas pela órbita da Lua. A linha dos nodos orbitais da Lua varre um ângulo de 360º em um período de 18.6 anos (chamado de ciclo de Saros). A figura abaixo ilustra este movimento da linha dos nodos orbitais da Lua.
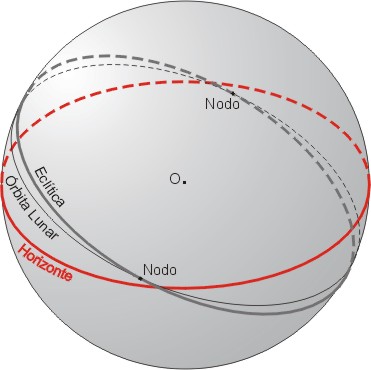
A figura abaixo mostra a eclítica e a órbita da Lua projetadas sobre a esfera celeste. Elas fazem um ângulo de 5.2° entre si. Este é o valor da inclinação da órbita da Lua em torno da Terra com relação ao plano orbital da Terra em torno do Sol. Os dois nodos orbitais da Lua são também mostrados. A linha que os conecta é a linha dos nodos e somente quando a Lua Cheia ou Nova ocorrem perto destas posições temos eclipses.
A próxima figura descreve os eclipses da Lua e do Sol usando os cones de sombra que a Lua e a Terra projetam no espaço. A luz do Sol vem da esquerda da figura. Quando a Lua está à esquerda da Terra, ela é nova, pois sua face iluminada é invisível para nós. A Lua cheia é representada à direita da Terra. No diagrama superior, as fases cheia e nova não levam a eclipses, pois o cone de sombra da Lua (da Terra) não se projeta sobre a Terra (Lua). Essas fases estão ocorrendo fora dos nodos orbitais, quando, portanto, o Sol não se situa ao longo da reta que liga a Terra à Lua. No diagrama inferior, por outro lado, os 3 astros estão alinhados, fazendo com que a sombra da Lua Nova se projete sobre uma pequena região da superfície da Terra (causando um eclipse do Sol nesta região) e com que a sombra da Terra se projete sobre a Lua Cheia (causando um eclipse lunar).
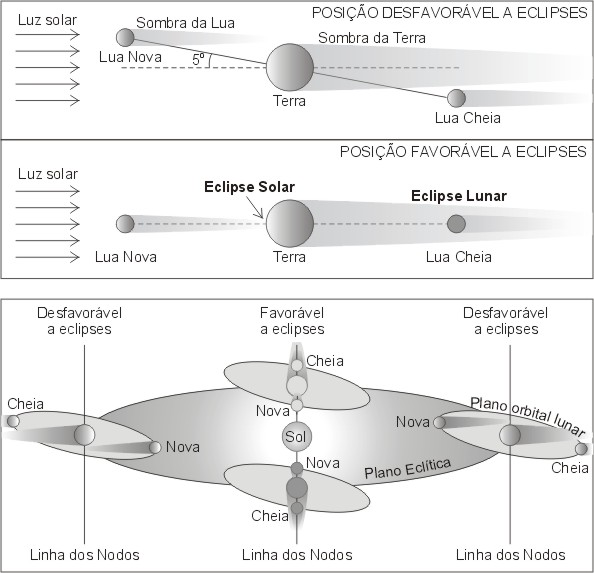
Já a figura acima combina os elementos orbitais e o jogo de sombras para mostrar a situação favorável à ocorrência de eclipses. A linha dos nodos orbitais da Lua é a linha que corta o centro da figura. Ao longo dela vemos que as fases nova e cheia da Lua acarretam eclipses. Já quando o Sol está fora da linha dos nodos (situações mostradas nas partes à esquerda e à direita da figura), as fases nova e cheia não levam a eclipses, pois o cone de sombra da Lua (da Terra) não é projetado sobre a Terra (a Lua).
A ocorrência de eclipses solares é devida a uma coincidência: o fato de que os diâmetros angulares da Lua e do Sol, vistos da Terra, são quase iguais.
Mas note que o diâmetro aparente da Lua varia ao longo do mês, pois sua órbita em torno da Terra é uma elipse moderadamente excêntrica; no apogeu (ponto da órbita em que a distância é máxima) a Lua parece ser 15% menor do que no perigeu (ponto de maior aproximação à Terra). Se ocorre um eclipse solar na primeira situação, a Lua não cobrirá todo o Sol, ocasionando um eclipse anular.Sistemas de Medida de Tempo
Nesta seção vamos estudar em mais detalhe as diferentes formas de se medir o tempo com base no movimento diurno dos astros. Veremos também a relação entre a hora local e a longitude do observador. Mas para atingirmos este objetivo, faz-se necessário definirmos alguns conceitos que parecem e são simples, mas por vezes resultam em alguma confusão.
Instante, Hora, Intervalo e Estado de um Cronômetro.
Uma possível fonte de confusão está em saber diferenciar conceitos como instante, hora e intervalo de tempo e compreender exatamente o que se quer dizer com essas definições. Todos nós temos uma noção cotidiana do tempo. Podemos ordenar, de acordo com nossa capacidade de memória, fatos e acontecimentos em seqüência no tempo. Esta noção do tempo, baseada na nossa experiência do dia a dia, nos faz "sentir" o tempo como algo que "passa" ininterruptamente, levando a uma sucessão constante e linear de instantes. Não abandonemos pois esta noção. Assim, definimos de forma genérica o tempo como uma variável cujo valor cresce de forma uniforme e que pode ser representada em um eixo. Um instante então pode ser entendido como um ponto ao longo do eixo do tempo. O valor numérico desta variável, o tempo, correspondente a cada instante nós chamamos de hora. Colocado de outra maneira, podemos identificar qualquer instante no eixo do tempo atribuindo-lhe um valor numérico que corresponde à hora naquele instante.
Mas há diferentes formas (ou sistemas) que podemos usar para atribuir uma hora a um dado instante. Ou seja, um determinado instante no tempo pode ser e é caracterizado por diferentes valores de hora. Já definimos anteriormente pelo menos dois sistemas de tempo, a cada um dos quais associamos uma determinada definição de hora: hora solar e hora sideral. Qualquer instante então é caracterizado por valores, em geral diferentes, de hora solar e de hora sideral.
Consideremos agora um outro conceito extremamente importante: o intervalo. Intervalo de tempo é a distância ao longo do eixo do tempo entre dois instantes. O valor do intervalo depende do sistema que estamos usando para marcar hora. O que veremos neste e no próximo capítulo são justamente diferentes definições de hora (ou dizendo em outras palavras, diferentes sistemas de tempo) e como converter um intervalo de tempo de um sistema para outro.
Como marcamos a hora associada a um dado instante? Em geral, usa-se um cronômetro. Existem tanto cronômetros siderais, que marcam a hora sideral, quanto cronômetros comuns, marcando a hora solar. Nem sempre a leitura do cronômetro nos dá exatamente a hora nestes sistemas. E isso nem é necessário, desde que saibamos converter a leitura feita no cronômetro em um dado instante (chamada de instante cronométrico, I) em hora sideral ou solar. A diferença entre a hora e o instante cronométrico é chamada de estado do cronômetro, E.
Hora = I + E
Por exemplo, S = IS + ES, onde S é a hora sideral num dado instante, IS é a leitura feita em um cronômetro sideral neste instante e ES é o estado deste cronômetro. Como determinar o estado de um cronômetro? Basta fazermos a leitura do instante cronométrico em um instante para o qual saibamos com precisão a hora. Por exemplo, ao observarmos uma estrela passar pelo nosso meridiano, sabemos que a hora sideral neste instante é igual à ascensão reta α da estrela: S = α. Se neste instante o cronômetro indica IS, seu estado será E = S - IS = α - IS.
Conhecido o estado do cronômetro em um dado instante, espera-se que ele se mantenha constante, pelo menos por algum tempo. Este certamente seria o caso de um cronômetro perfeito. Na prática, há variações em E ao longo do tempo, que quantificam aquilo que chamamos de marcha (m) de um cronômetro:
m = ΔE / ΔHora
Quanto menor a marcha, mais regular é o cronômetro, mais fácil portanto será usá-lo para determinar a hora. Como veremos neste capítulo, a marcha de um relógio de césio, que mede o tempo atômico, é da ordem de m = 1 / 1.000.000.000 = 10-9.
As diferentes definições de hora
Vimos que, através da observação do movimento diurno dos astros, em especial pela determinação do ângulo horário, podemos medir o tempo. Vimos os conceitos de hora sideral e solar, baseadas, respectivamente, nos ângulos horários do ponto Vernal (ponto γ) e do Sol.
S = Hγ
M = Hsol + 12h
Ou seja, à medida em que a Terra rotaciona, variam os valores de ângulo horário tanto do Ponto Vernal quanto do Sol, variando portanto os valores de hora sideral e solar. A cada instante no tempo, portanto, podemos atribuir um valor de cada uma destas definições de hora. Outra consideração importante é que, sendo o ângulo horário contado a partir de um dado meridiano, o valor de ângulo horário do Sol ou do ponto γ em um dado instante é diferente de um meridiano para outro.
Nós já vimos também que, pelo fato de o Sol mover-se por entre as estrelas, ao longo da eclítica e de oeste para leste, a uma taxa média de 360/365.25 = 0.9856° por dia, o dia solar é mais longo do que o dia sideral. Ou seja, o intervalo entre duas culminações superiores sucessivas do Sol é 3m56.04s mais longo do que o intervalo entre duas culminações superiores sucessivas de uma estrela, pois o Sol está constantemente se deslocando no sentido contrário ao movimento diurno. Note que a hora que marcamos no relógio, como veremos a seguir, é ligada (mas não é idêntica) à hora solar, de forma que outra maneira de dizer a mesma coisa é afirmar que uma dada estrela passa pelo meridiano de um observador 3m56.04s "mais cedo" a cada dia.
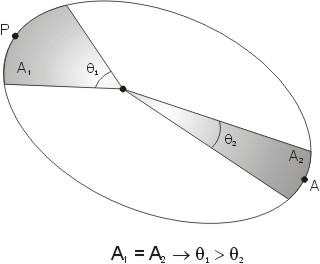
Na verdade, existe mais de uma definição de hora solar. O motivo é que o movimento do Sol ao longo da eclítica não se dá uniformemente, ou seja, a velocidade angular com que o Sol se desloca ao longo da eclítica varia com a época do ano. Isso porque o movimento do Sol ao longo da eclítica é o reflexo do movimento orbital da Terra no espaço em torno dele. Sendo a órbita da Terra uma elipse, sua velocidade angular orbital varia, sendo maior no periélio e menor no afélio. Esta situação é bem representada na figura abaixo, onde a elipse representa a órbita da Terra em torno do Sol. Este último, de acordo com a 1a Lei de Kepler, se situa em um dos focos da órbita terrestre. O ponto P, de máxima aproximação ao Sol é o periélio, enquando que o ponto A, de maior distância, é o afélio. Na figura vemos dois arcos, θ1 e θ2, varridos pela Terra em sua órbita quando próxima do periélio e do afélio, respectivamente. Pela 2a Lei de Kepler , sabemos que as áreas A1 e A2 varridas pela Terra são iguais se o intervalo de tempo decorrido ao varrê-las for o mesmo. Como próximo do periélio a distância Sol-Terra é mínima, a velocidade angular tem que ser máxima para manter constante a área varrida. Logo, o deslocamento angular do Sol sobre a eclítica também é variável.
Claro que esta situação não é muito conveniente em termos de marcação da hora: não queremos ter dias com mais de 24h e outros com menos de 24h, seria muito confuso!
Para contornar este problema, definimos uma hora solar verdadeira (V) e uma hora solar média (M). Somente a primeira é baseada no ângulo horário do objeto luminoso que vemos no céu e que chamamos de Sol. A hora solar média é baseada no ângulo horário do Sol Médio. O Sol Médio é um sol imaginário, mais bem comportado do que o Sol verdadeiro. Sua velocidade angular de deslocamento no céu é constante e, portanto, seu ângulo horário varia uniformemente. Os valores de hora solar verdadeira, V, e média, M, são dados portanto por:
V = HV + 12h
M = HM + 12h
onde HV e HM são, respectivamente, os ângulos horários do Sol verdadeiro e do Sol médio.
Outra definição importante de hora é a de tempo universal (TU). Tempo universal é simplesmente a hora solar média no meridiano de Greenwich (longitude λ = 0°). Sabemos que a hora associada a um determinado instante no tempo, seja sideral ou solar, verdadeira ou média, não é a mesma em todos os pontos da Terra. Ela varia com a longitude, ou seja, com o meridiano. Isso é fácil de entender, uma vez que se um astro (sol verdadeiro, sol médio ou o ponto vernal) está passando pelo meridiano a uma dada longitude λ1, ele certamente não poderá estar passando pelo meridiano a uma longitude λ2, exceto se λ1 = λ2. Se em λ1, HM = 0°, por exemplo, em λ2 = λ1 + Δλ, HM = Δ λ. Ou seja, a diferença de hora entre dois meridianos em um dado instante é igual à diferença de longitude entre os dois meridianos. Como dissemos, isso vale para qualquer sistema de medida de tempo.
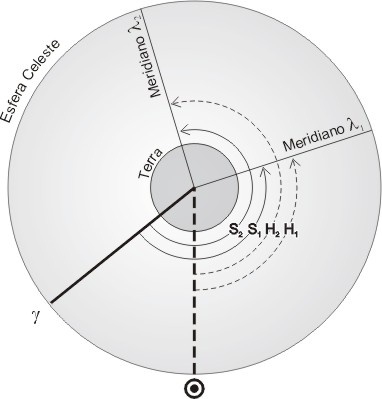
A figura abaixo ilustra este fato, mostrando a Terra vista de cima da direção do pólo norte. Vemos na figura dois meridianos, de longitudes λ1 e λ2, respectivamente. O círculo mais externo é a esfera celeste e nela estão indicadas a posição do ponto γ e do Sol Médio em um dado instante. O movimento diurno se dá no sentido horário, sendo portanto nesta direção que contamos os valores de ângulo horário. Basta olhar para a figura para constatar que vale a igualdade:
ΔS = S2 - S1 = λ2 - λ1 = H2 - H1 = M2 - M1 = ΔM
Note que se arbitrarmos que a longitude cresce para oeste, sendo nula no meridiano de Greenwich, teremos que λ2 < λ1 . Logo, é necessário modificar ligeiramente a relação entre diferença de hora e diferença de longitude:
ΔS = S2 - S1 = λ1 - λ2 = H2 - H1 = M2 - M1 = ΔM
A inversão na posição das longitudes na expressão acima faz com que uma diferença positiva de hora (meridiano λ2 a leste de λ1) corresponda a uma diferença positiva em longitute.
Dessa forma, podemos estabelecer uma relação simples entre a hora solar média M de um local cuja longitude é λ e a hora universal TU:
ΔM = M - TU = 0° - λ = - λ
Logo,
M = TU - λ
O sinal negativo resulta dessa nossa convenção de contar a longitude positivamente para oeste, de forma que pontos de longitude λ > 0° estão atrasados com relação ao meridiano de Greenwich. Por exemplo, se são 9h solares médias em Greenwich, TU = 9h, qual o valor de M no meridiano de longitude λ = -75°? Trata-se de um meridiano a leste de Greenwich (longitude negativa), de forma que sua hora solar média tem que ser adiantada com relação a este último. Pela expressão acima, de fato teremos:
M = TU + 75° = 9h + 5h = 14h
Qual a hora que marcamos no relógio? Essa pergunta procede, principalmente à medida em que introduzimos cada vez mais sistemas de contagem do tempo. Resposta: a hora do relógio é a hora legal (HL). A hora legal é baseada no movimento do Sol Médio, mas obedece a várias conveniências geo-políticas. A hora solar média M varia continuamente com a longitude. Em outras palavras, a hora solar média no Rio de Janeiro é diferente da de São Paulo por alguns minutos, pois esta é a diferença de longitude entre os meridianos que passam pelas duas cidades. Não seria conveniente para o comércio, indústria, política, etc que os cariocas acordassem um pouco mais cedo, e começassem a terminassem de trabalhar também um pouco mais cedo, simplesmente por que o Sol passa pelo seu meridiano astronômico alguns minutos antes do que pelo meridiano dos paulistas. Necessidades de se padronizar a hora em grandes regiões unidas econômica, cultural e politicamente levaram à definição de grandes faixas de longitude, chamadas de fusos horários (F), que compartilham de uma mesma hora legal. Pela convenção dos fusos horários, a superfície da Terra é dividida em 24 fusos, compreendendo um domínio de 15° de longitude cada. O primeiro fuso (F=0h) é aquele cujo centro contém o meridiano de Greenwich (λ = 0°). Contrariamente ao que fazemos com a longitude, a oeste (leste) de Greenwich os fusos são contados negativamente (positivamente). Uma representação esquemática dos fusos horários é dada pela figura abaixo. Nela vemos, em linhas tracejadas, o meridiano de Greenwich, correspondente ao fuso F = 0h. Na direção leste temos contados os fusos positivos, até F = +12h, junto à linha de mudança de data (λ = +/-180°). A oeste, temos os fusos negativos, sendo que novamente F = -12h encontra-se imediatamente a leste da linha internacional de mudança de data. 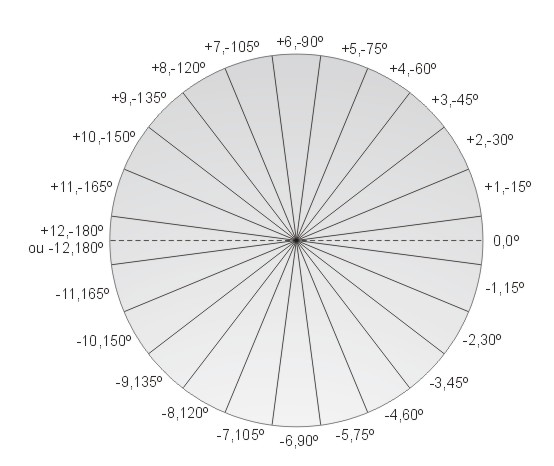
Qual a relação entre a hora legal, que marcamos no relógio, e a hora solar média M? Trata-se de uma relação muito simples, que apenas reflete a definição de hora legal como sendo a hora solar média no meridiano central de um fuso. Logo,
M - HL = ΔM = - Δλ
M = HL - Δλ
onde Δλ neste caso é simplesmente a diferença de longitude entre o meridiano do observador e o meridiano central do fuso horário em que este observador se situa. Considere o caso de um observador em Porto Alegre, cuja longitude é aproximadamente λPOA = 51° (lembre-se que estamos sempre considerando longitudes como positivas a oeste de Greenwich). Como vimos, o centro do fuso F = -3h corresponde a λ = 45°. Logo, Δλ = 51° - 45° = 6°. Esta diferença positiva em longitude significa que Porto Alegre está a oeste do meridiano central do fuso F=-3. Assim, a hora solar média em Porto Alegre está atrasada com relação a este último:
M = HL - 6° = HL - 24m.
Se em um dado instante a hora legal no fuso de -3h é HL=15h, sabemos que a hora solar média no meridiano de Porto Alegre é MPOA = 14h36m. O ângulo horário do Sol médio com relação a este meridiano será então HM,POA = MPOA - 12h = 2h36m.
Qual a relação entre hora legal HL em um dado meridiano de longitude λ e o tempo universal ? Esta relação é igualmente simples:
HL = TU + F
onde F é o fuso onde se situa o meridiano de longitude λ.
Também é fácil provar esta expressão, lembrando que a diferença HL - TU nada mais é do que a diferença de hora solar média entre dois meridianos centrais, um no fuso F (λc) e outro em Greenwich (λ = 0°). Logo:
ΔM = HL - TU = 0° - λc = F
Ou seja, no instante em que são 15h no fuso que contém a maior parte do território brasileiro (F = -3h), a hora universal será TU = HL - F = 15h + 3h = 18h.
O tempo sideral também pode ser definido de mais de uma maneira. Veremos mais adiante que a posição do ponto γ não é rigorosamente fixa entre as estrelas, devido a vários efeitos seculares como a precessão e a nutação. Se consideramos apenas a variação de posição do ponto vernal causada pela precessão, falamos em ponto vernal médio. Se incorporarmos os efeitos de nutação, teremos então o ponto vernal verdadeiro ou aparente. Assim , podemos falar de hora sideral média ou verdadeira. A diferença entre ambas é chamada de equação dos equinócios (q):
q = SV - SM = HγV - HγM
Tanto a hora solar quanto a sideral são exemplos de sistemas de medida de tempo baseados no movimento de rotação da Terra. São, portanto, chamados de sistemas rotacionais de medida de tempo. Mas existem maneiras de se contar o tempo que não dependem da posição de algum astro no céu com relação ao meridiano do observador. O tempo atômico, por exemplo, não é rotacional, já que é baseado nas transições atômicas de átomos de Césio 133. No intervalo de um segundo de tempo atômico ocorrem 9.192.631.770 transições de átomos de Ce 133 entre dois níveis hiperfinos de sua energia interna. Essa é a definição mais moderna de 1s.
Os sistemas rotacionais sofrem de algumas irregularidades, algumas delas previsíveis outras não. O movimento do pólo, por exemplo, afeta a longitude de qualquer ponto na superfície da Terra, o que se reflete no ângulo horário do Sol ou do ponto vernal (ver capítulo sobre variação de coordenadas equatoriais). Além disso, a velocidade angular de rotação da Terra não é uniforme. Há uma lenta tendência de desaceleramento da rotação, causada pelo atrito da massa líquida do planeta, que tende a se alinhar com a Lua e o Sol devido às marés, com a parte sólida. Além disso há variações sazonais, provavelmente causadas por mudanças meteorológicas, na rotação do planeta. Finalmente há componentes irregulares na variação da rotação, ainda não explicados de maneira satisfatória.
Diantes das irregularidades mencionadas acima, podemos na verdade definir 3 tipos de sistemas de tempo universal:
TU0: baseado apenas no valor do ângulo horário do Sol Médio medido por um observador no meridiano de Greenwich.
TU1: TU0 corrigido para o efeito de variação da longitude, Δλ, causado pelo movimento do pólo (ver capítulo sobre variação de coordenadas equatoriais).
TU1 = TU0 + Δλ
TU2: TU1 corrigido para as variações sazonais na velocidade angular de rotação da Terra, ω:
TU2 = TU1 + Δω(°)/15.
Já o tempo atômico é muito mais regular do que qualquer sistema rotacional de medida de tempo. A regularidade da contagem do tempo usando transições de átomos de Césio, por exemplo, é da ordem de 1 parte em 1 bilhão. Ou seja, após 1 bilhão de segundos (mais de 30 anos), a incerteza na contagem do tempo atômico é de apenas um segundo. Por outro lado, o tempo atômico está menos sintonizado com a posição do Sol no céu. Assim, a discrepância entre o tempo atômico e o tempo rotacional tende a aumentar. Para evitar uma desvinculação muito grande entre o tempo atômico e o solar, faz-se necessária a definição do tempo universal coordenado (TUC). O TUC é um sistema de tempo atômico que sofre correções periódicas para manter-se em consonância com o tempo universal, mais especificamente o TU1.
Existem ainda outros sistemas de tempo. O tempo das efemérides, por exemplo, é a variável independente que entra nas expressões que nos dão a posição de planetas e de seus satélites em algum sistema de coordenadas conveniente, como o sistema de coordenadas eclíticas. À medida em que somos capazes de formular modelos mais sofisticados para descrever os movimentos de planetas em torno do Sol e de satélites em torno de seus planetas, o tempo das efemérides se torna mais fácil de ser obtido, sendo também uma medida de tempo independente da rotação da Terra.
Conversão entre Sistemas de Medida de Tempo
Sabemos que um dia solar médio tem 24h solares de duração, cada hora solar dividida em 60 minutos (solares) e 3600 segundos (solares). Estes são os intervalos de tempo usados em nossa vida cotidiana. Expresso nessas unidades, o dia sideral tem uma duração de 23h56m04.090538s. Mas podemos definir intervalos como hora, minuto e segundo siderais, de forma que o dia sideral tenha 24h siderais. Claro que a unidade de tempo sideral necessariamente será sempre mais curta do que a unidade solar. Uma questão importante e recorrente em determinações astronômicas é a de como converter intervalos de tempo expressos em unidades siderais em solares ou vice versa.
Conversão de tempo solar em sideral
Suponha que tenhamos um intervalo ΔS de tempo sideral. Queremos saber qual o valor ΔM deste mesmo intervalo em unidades de tempo solar.
Para melhor entendermos por que o mesmo intervalo tem valor numericamente maior em unidades siderais do que solares médias, basta lembrarmos que o tempo é baseado, em ambos os sistemas, em valores de ângulo horário: do ponto γ (Sol Médio) no caso do sistema sideral (solar médio).
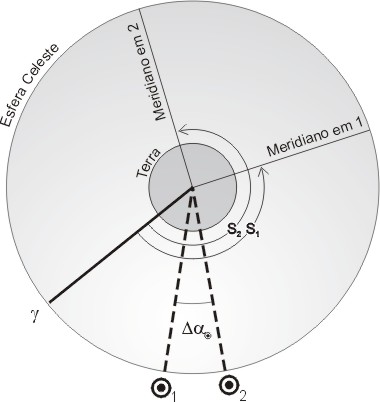
Na figura acima mostramos o intervalo, expresso em unidades siderais, ΔS = S2 - S1 decorrido entre dois instantes no tempo. Neste intervalo, o meridiano de um observador, devido à rotação da Terra, varreu exatamente este ângulo ΔS no espaço. Isso porque o observador é móvel, enquanto o ponto Vernal pode ser considerado como fixo na esfera celeste durante o intervalo. Já a posição do Sol Médio, se deslocará ligeiramente para leste, devido ao movimento anual do Sol. Sua ascensão reta aumentará então por Δα(°) = ΔS(°) / 366.25, onde 366.25 é o número de dias siderais no ano. Assim, o valor do mesmo intervalo em unidade solares médias, ΔM, será menor:
ΔM = ΔS - Δα = ΔS (1 - 1 / 366.25) = ΔS (1 - 0.00273043359) = ΔS (1 - μ)
onde μ = 1/366.25 = 0.00273043359.
O mesmo fator de conversão pode ser obtido lembrando que um dia sideral tem 24h siderais (por definição de hora sideral), mas apenas 23h56m04.090538s solares médios. Logo, temos a regra de proporcionalidade:
ΔS / ΔM = 24h / 23h56m04s = 1.00273790926 = 1 + η
onde η = 0.00273790926. Note que é válida a relação:
(1 + η)(1 - μ) = 1
Assim, se conhecemos a hora sideral em um dado meridiano em um determinado instante, S0, e desejamos conhecer a hora sideral S no mesmo meridiano decorrido um intervalo em hora solar igual a ΔM, teremos:
ΔS / ΔM = 1 + η ---> ΔS = S - S0 = (1 + η) ΔM
S = S0 + (1 + η) ΔM
É comum, por exemplo, querermos conhecer a hora sideral S às M horas solares médias locais em um determinado meridiano de longitude λ. Sabemos que se são M horas solares médias locais nesta longitude, o tempo universal neste instante será TU = (M+λ) (como de hábito adotamos a convenção de que λ > 0° a oeste de Greenwich e λ <>0 em Greenwich correspondente a TU=0h para o dia em questão. Em unidades solares médias, ter-se-ão decorrido ΔM = (M+λ) horas desde este instante. O intervalo em horas siderais correspondente será, portanto:
ΔS = ΔM (1 + η) = (M + λ) (1 + η)
A hora sideral em Greenwich, SG, no instante desejado será portanto:
SG = S0 + ΔS = S0 + (M+λ)(1+η)
Mas queremos a hora sideral S no meridiano de longitude λ e não em Greenwich (λ = 0°). Precisamos então subtrair a diferença em longitude:
S = SG - λ = S0 + (M+λ)(1+η) - λ = S0 + (M+λ)η + M; eq. (1)
A expressão acima nos dá exatamente o que queríamos: a hora sideral em um meridiano de longitude λ dada e no instante em que a hora solar média local é M. Como já mencionado, o valor de S0, a hora sideral em Greenwich (λ = 0°) à TU=0h é listada, dia a dia no ano, no Anuário Astronômico do Observatório Nacional (ON) ou no Astronomical Almanac.
Exemplo de tabela do Anuário do ON com valores de S0
Exemplo de tabela do Astronomical Almanac com valores de S0
A fórmula acima é bastante geral. Suponha que queiramos simplesmente a hora sideral em Greenwich a uma hora solar média local M. Como se trata do meridiano de Greenwich, a hora solar média local é também a hora universal: TU = M. Além disso, λ = 0h. Logo, a hora sideral desejada será:
S = S0 + M (1+η) = S0 + TU (1+η)
onde S0 é a hora sideral em Greenwich à 0h TU (que pode ser encontrada em Efemérides) e η = 0.00273790926.
Outro exemplo: provar que a hora sideral S em um meridiano de longitude λ à M=0h solar média local é dada por:
S = S0 + λη
onde, como sempre, S0 é a hora sideral em Greenwich a TU = 0h.
Consideremos ainda uma situação, bastante comum, em que temos que escolher uma estrela para observação em um determinado dia e intervalo de hora legal. A ocasião mais favorável para observarmos uma estrela é, em geral, próxima do instante de sua culminação superior, quando sua altura no céu é máxima. Suponha que tenhamos o intervalo de hora legal compreendido entre HL1 e HL2 (HL2 > HL1) para a observação. Inicialmente temos que converter hora legal HL em hora solar média local M. Como vimos, a diferença entre as duas será igual à diferença entre a nossa longitude, λ, e a longitude do meridiano central do fuso horário em que nos encontramos, λc.
M1 - HL1 = λc - λ ====>>> M1 = HL1 + λc - λ
M2 - HL2 = λc - λ ====>>> M2 = HL2 + λc - λ
Os valores de hora sideral S1 e S2, correspondentes, respectivamente, a M1 e M2, serão dados pelas expressão (1) acima, sendo que o valor de S0 , a hora sideral em Greenwich à TU=0h, é sempre tirado das efemérides. Como sabemos que a culminação de uma estrela ocorre à hora sideral igual à sua ascensão reta, α, temos que escolher nosso alvo usando o critério em ascensão reta S1 < α <>2.
Conversão de tempo sideral em solar
Suponha agora que queiramos fazer o inverso: determinar a hora solar média local, M, dada a hora sideral S num dado instante. Basta resolvermos a equação (1) acima para M:
M = (S - S0 - λη)/(1+η).
Como (1 - μ) = 1/(1 + η),
M = (S - S0 - λη) (1-μ)
onde μ =0.00273043359.
Equação do Tempo
A rotação da Terra nos proporciona uma unidade natural de tempo: o dia. Vimos que podemos definir o dia solar, por exemplo, como o intervalo entre duas passagens meridianas do Sol. Já o dia sideral é o intervalo decorrido entre duas passagens meridianas de uma estrela ou do ponto γ. Vimos que em um dia, solar ou sideral, o ângulo horário do astro usado como referência varia de 0° a 360° (ou de 0h a 24h).
Na prática, se medirmos, com um cronômetro ou relógio, a duração do dia solar, notaremos que ela varia. Em outras palavras, o dia solar não tem uma duração fixa. Já discutimos a causa desta variação na duração do dia solar: entre outras coisas, ela se deve ao fato de que o Sol caminha ao longo da eclítica com velocidade variável; quando a Terra está no periélio (ou seja, sua distância ao Sol é mínima), a velocidade angular do Sol sobre a eclítica é máxima, fazendo com que o dia solar seja de maior duração. Já quando a Terra está no afélio, a velocidade angular do Sol na eclítica é mínima, o que torna o dia solar igualmente mínimo. Outro motivo que explica a variação observada do dia solar é o de que a hora solar depende do ângulo horário do Sol, Hsol , medido portanto ao longo do equador celeste. Mas o movimento do Sol se dá sobre a eclítica. Assim, mesmo que sua velocidade angular ao longo desta última fosse constante (ou seja, se a órbita da Terra fosse perfeitamente circular), sua projeção sobre o equador celeste não o seria.
Um dia solar que não seja sempre de 24h não é muito conveniente para regular a vida das pessoas. A solução para este problema foi definir um Sol Médio. O Sol Médio é bem comportado: ele caminha com velocidade angular constante e sobre o equador celeste. Assim, duas culminações superiores do Sol Médio estarão sempre separadas no tempo pelo mesmo intervalo, chamado de dia solar médio. Este tem sempre a duração de 24h tais como contadas por um cronômetro ou relógio comuns. A diferença entre o dia solar verdadeiro e o médio é chamada de equação do tempo. Abaixo vemos a equação do tempo graficada ao longo do ano.
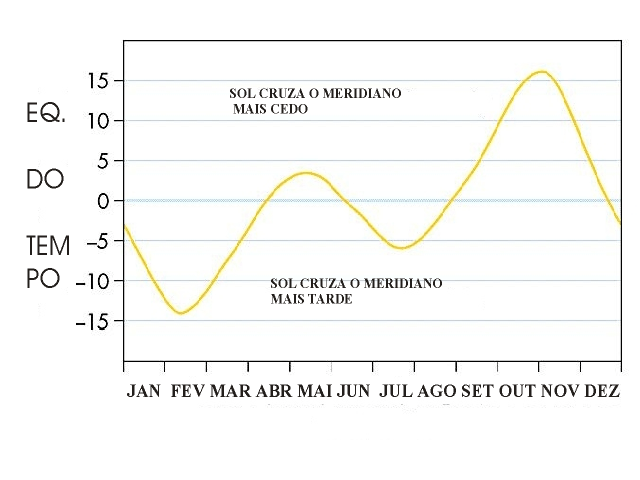
Vemos, portanto, que a equação do tempo atinge valores de mais do que 15 minutos em determinadas épocas do ano. Geralmente representamos a equação do tempo pela letra E (às vezes usa-se o equivalente grego ε). De qualquer forma não confunda equação do tempo com estado de um cronômetro apenas porque usamos a mesma notação! Matematicamente temos que:
E = Hsol med - Hsol ver = αsol ver - αsol med
Na verdade, de acordo com esta definição, o gráfico acima representa -E. A segunda igualdade acima resulta do fato de que a hora sideral pode ser expressa tanto com o Sol Médio quanto com o Verdadeiro: S = Hsol ver + αsol ver = H sol med + αsol med.
Os valores de E também podem ser encontrados nas efemérides astronômicas:
Valores da Eq. do Tempo no Anuário do ON
Valores da Eq. do Tempo no Astronomical Almanac
Equação do Centro
Além do Sol Médio, os astrônomos conceberam um outro sol imaginário, o Sol Fictício. O Sol Fictício percorre a eclítica, assim como o Sol Verdadeiro. A diferença é o que o primeiro o faz a velocidade angular constante. Se os dois partem juntos do periélio (que atualmente ocorre em torno do dia 04/01), o Sol Verdadeiro inicialmente terá uma dianteira, já que no periélio sua velocidade é máxima. Assim, entre o periélio e o afélio (que ocorre no início de julho), o Sol Verdadeiro percorre a eclítica à frente do Sol Fictício. Este intervalo de tempo inclui a passagem pelo ponto γ, em março. Os dois sóis chegam juntos ao afélio e, a partir daí e até o próximo periélio, o Sol Fictício caminha na frente, já que no afélio a velocidade do Sol Verdadeiro é mínima.
A situação é representada na figura abaixo. Nela S f e S v representam as posições do Sol Fictício e do Verdadeiro, respectivamente. P' e A' são os pontos da órbita da Terra correspondentes ao periélio e ao afélio. Os pontos marcados por β representam os solstícios de inverno e verão. Define-se como equação do centro (U) a diferença entre as longitudes eclíticas do Sol Verdadeiro e do Sol Fictício.
U = λv - λf
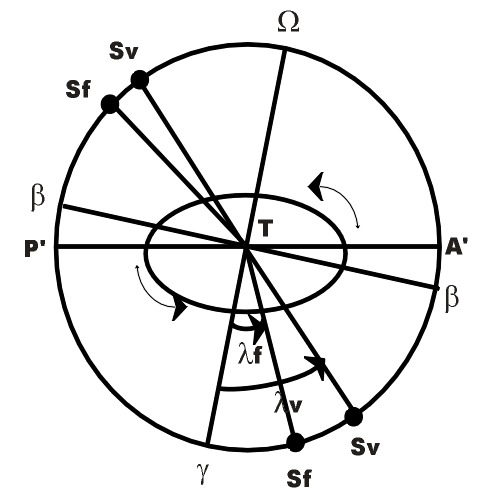
Assim, U > 0 (λv > λf) entre o periélio e o afélio (de janeiro a julho) e U <>v < λf) entre afélio e o periélio (de julho a janeiro).
Redução ao Equador
Outra definição importante é a chamada redução ao equador (Q). Esta é definida como a diferença entre a ascensão reta do Sol Verdadeiro e sua longitude eclítica.
Q = αv - λv
Na figura abaixo vemos as três equações, U, Q e E, graficadas em função do dia ao longo do ano. É fácil provar, com as definições destas equações, que
E = U + Q
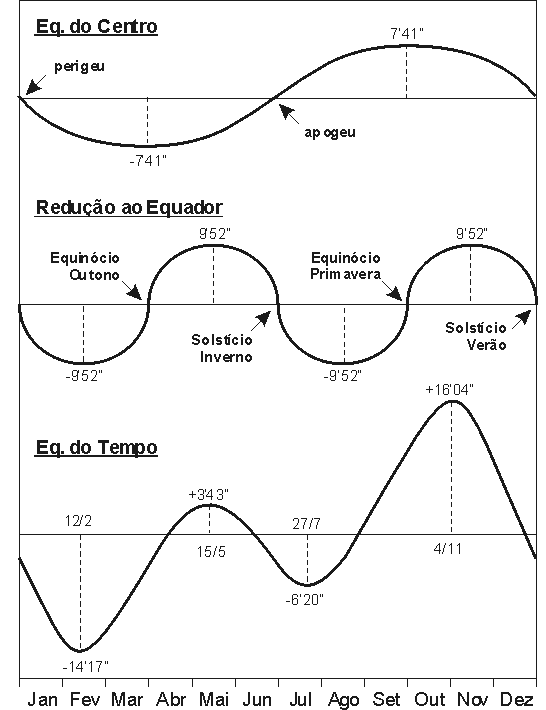
BY→Isis

Um comentário:
Só um problema quem conseguirá ler tudo isso??
Postar um comentário